Mathapedia
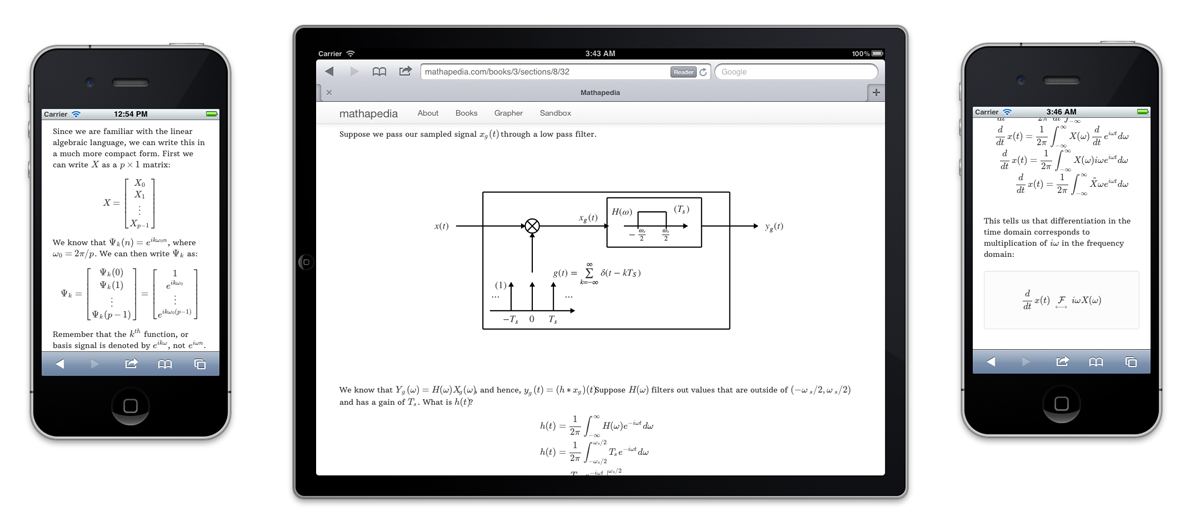
Author interactive math textbooks online using LaTeX and PSTricks in real-time
This project extends the great work of MathJax to enable real-time, dynamic authorship of mathematical ebooks — rendered by LaTeX2JS.
Consistent diagrams and mathematics on PDF or any device
Works on iPhone, iPad, Nexus Tablets, and Androids.
Author for both interactive Web and Paper
Remember paper? Well, now you can have the best of both worlds.
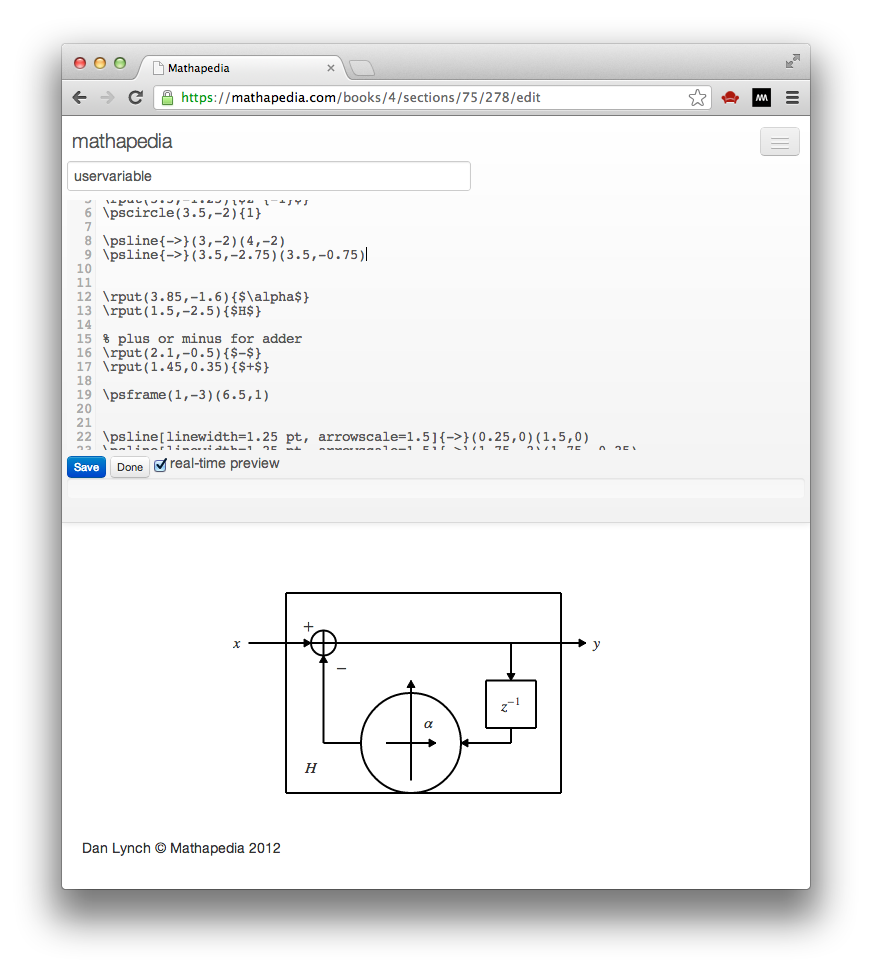
Author PSTricks graphics in real-time
The real-time editor gives you instantaneous feedback with consistent PSTricks drawing capabilities.